How To Leverage Ansetry.com Data For Your Genetic Makeup

• Methodology Commodity
• Open Access
• Published: 16 January 2015

Fast private ancestry inference from Dna sequence data leveraging allele frequencies for multiple populations

BMC Bioinformatics volume 16, Article number:four (2015) Cite this article

• 6975 Accesses

• 29 Citations

• 3 Altmetric

• Metrics details

Abstract

Background

Estimation of individual beginnings from genetic data is useful for the analysis of disease association studies, agreement human being population history and interpreting personal genomic variation. New, computationally efficient methods are needed for ancestry inference that tin can finer utilize existing data about allele frequencies associated with different man populations and tin can work directly with DNA sequence reads.

Results

We describe a fast method for estimating the relative contribution of known reference populations to an individual'south genetic beginnings. Our method utilizes allele frequencies from the reference populations and individual genotype or sequence information to obtain a maximum likelihood estimate of the global admixture proportions using the BFGS optimization algorithm. It accounts for the uncertainty in genotypes present in sequence data past using genotype likelihoods and does non crave individual genotype information from external reference panels. Simulation studies and application of the method to real datasets demonstrate that our method is significantly times faster than previous methods and has comparable accuracy. Using data from the 1000 Genomes project, we show that estimates of the genome-wide average ancestry for admixed individuals are consequent betwixt exome sequence data and whole-genome low-coverage sequence data. Finally, we demonstrate that our method tin be used to estimate admixture proportions using pooled sequence data making information technology a valuable tool for decision-making for population stratification in sequencing based clan studies that utilize DNA pooling.

Conclusions

Our method is an efficient and versatile tool for estimating ancestry from Deoxyribonucleic acid sequence information and is available from https://sites.google.com/site/vibansal/software/iAdmix.

Background

Allele frequencies at most loci in the human genome differ between populations as a upshot of human demographic history and genetic drift [one]. Individuals can be grouped into genetic clusters that correspond to major geographic regions using information about genotypes at multiple loci [2]. Individuals whose ancestors originated in different populations, and who are, therefore, admixed, showroom ancestry associated with multiple different genetic clusters or populations. For case, the majority of African Americans possess 10-20% of their genetic beginnings consequent with European genetic background with the remainder of their beginnings being African [three].

Estimating the unknown admixture proportions of an individual is valuable for understanding homo population history as well as controlling the rate of faux associations in disease association studies by avoiding or correcting for population stratification, i.e. differences in ancestry between cases or controls [4,5]. A widely used arroyo to correct for population stratification is to include estimates of admixture proportions for each individual as covariates in statistical models testing for clan [six].

2 types of methods take been developed for the assay of beginnings and population construction using genetic data: model-based clustering methods such as Construction [7], FRAPPE [viii] and ADMIXTURE [9], and principal component analysis (PCA) [ten]. Model-based clustering methods model a population using allele frequencies at multiple loci and each individual's genome equally an admixture of alleles from different populations.

Given a stock-still number of clusters (populations), K, these methods use an unsupervised clustering approach to simultaneously infer the allele frequencies associated with the M clusters and guess the relative contribution of the M clusters to each individual'south ancestry. The low cost of whole-genome genotyping assays has enabled comprehensive surveys of genetic variation and these methods have been highly successful in understanding the population structure in many different human being populations [xi-15].

Most existing methods for assay of admixture and beginnings have been designed to clarify population structure in an unsupervised fashion. Supervised analyses of admixture tin be valuable for estimating authentic admixture fractions for individuals whose ancestral history is known. For example, authentic admixture fractions for African American individuals associated with European and African bequeathed populations tin be obtained using ADMIXTURE and similar software only if European and African individuals are included as reference. Alexander and Lange [16] have extended ADMIXTURE to behave out supervised analysis by including genotype data for individuals who belong to predefined population clusters. Nonetheless, supervised analyses of an individual's genetic ancestry can be performed using population allele frequencies lone and does not necessarily require private level genotype information.

Another limitation of existing methods is that these methods were designed to process data generated from genotyping arrays and crave precise noesis of the genotypes for each individual. Equally a consequence, these methods are not well suited to inferring ancestry from DNA sequence data where the genotypes may non be known precisely. As the cost of Deoxyribonucleic acid sequencing has decreased rapidly, high-throughput sequencing instruments such as the Illumina HiSeq are being used to sequence large number of man genomes and disease clan studies are beingness pursued using high-throughput sequencing instead of genotyping arrays [17]. Sequencing the entire human genome can still exist too plush, and many studies perform low-depth sequencing to obtain information almost variants and genotypes. For example, the m Genomes project has performed low-coverage (2-4 x) whole-genome sequencing for thousands of individuals from diverse populations [18]. Other studies utilize targeted sequencing where merely specific regions of the genome, e.g. the coding regions of genes, are targeted for sequencing. Interestingly, a pregnant fraction of the reads derived from targeted sequencing fall outside of the targeted regions. Various studies have shown that thirty-50% of the reads map outside target regions [19]. Each off-target read that covers a single nucleotide polymorphism (SNP), for which reference population allele frequency information exists, is weakly informative almost the genotypes of the individual, and can be used to infer beginnings.

With the increasing utilise of high-throughput sequencing for studies of human being disease and population history, there is a demand for computationally efficient methods for ancestry inference that tin finer utilize existing information about allele frequencies associated with unlike human populations and tin work non only with genotypes but also with DNA sequence reads. Recognizing this challenge, several methods for beginnings inference from sequence data have recently been developed [20-22]. The NGSadmix method [20] essentially extends the ADMIXTURE method to work direct with sequence data using genotype likelihoods. Wang et al. [22] have developed a new method for estimation of individual genetic beginnings using analysis of sequence reads that compares each sequenced individual to a reference panel of individuals using chief-component assay (PCA). This method simulates sequence reads for each reference individual and uses the simulated information to build a PCA map which is projected back to the original PCA space. In this paper, nosotros propose a computationally fast method for estimating an individual's global (genome-wide) ancestry using genotype or sequence data and pre-determined population allele frequencies associated with multiple reference populations. Our method directly incorporates the dubiety in genotypes by working with genotype likelihoods calculated from aligned sequence reads. Our method has some similarities with NGSadmix in the use of genotype likelihoods to capture uncertainty in genotypes and with LASER in the use of a reference panel of individuals to estimate individual ancestry from sequence data. However, different these methods, information technology does not crave individual genotype data for the reference populations. Using allele frequencies has two advantages: (i) information technology eliminates the need for the reference console of individuals and the individual(s) being analyzed to have the same type of genetic information (genotypes vs sequence reads) and (two) the reference panel of individuals does not need to be analyzed again which leads to significant gains in computational efficiency.

Using false datasets, we demonstrate that our method can accurately infer admixture proportions for an individual with admixture from multiple continental populations. Using genotype data from the Human Genome Diversity Project, we show that the estimates of global genetic ancestry obtained using our method are consistent with those estimated using an existing method. Using sequence data for admixed individuals from the m Genomes Project, we demonstrate that the admixture estimates are high concordant between whole genome sequence data and exome data. In add-on, our technique compares very favorably with existing methods in terms of computation fourth dimension. This allows us to extend our method to estimate a parsimonious ready of admixture coefficients using an iterative arroyo.

Methods

Previous methods for model-based ancestry analysis [7-9] perform an unsupervised analysis of the ancestry of multiple individuals and jointly estimate allele frequencies for K (where K is user-defined) bequeathed populations and the relative contribution of each bequeathed population to each individual's genome. In contrast, our focus is on estimating the beginnings for a single individual using information about allele frequencies at a large number of loci for multiple reference populations. The allele frequencies for the reference populations can potentially be obtained from previous unsupervised admixture analysis of individuals from different human populations. Given an individual's genotypes at these loci, our goal is to approximate the admixture coefficients for each population, i.e. the fraction of the individual's genome that is derived from that population. We advise to estimate the admixture coefficients using the maximum likelihood method.

Likelihood model for admixture coefficients: We assume that all polymorphic sites are bi-allelic. Given a SNP with 2 alleles a and b, a diploid individual can have one of three possible genotypes: aa, ab and bb. Nosotros correspond the genotype Thou _i for an private at SNP i every bit the number of a alleles (0,1 or 2). Permit q _ij denote the allele frequency of the a allele at the i-th SNP in population j. Given k reference or bequeathed populations with known allele frequencies, let a _j represent the admixture proportion for the j-th population and A=[a _one,a _two,…,a _k ] be the vector of admixture coefficients. Nosotros ascertain \(f_{i} = \sum _{j=1}^{thou} q_{\textit {ij}}a_{j}\) every bit the weighted allele frequency at SNP i given the allele frequencies and admixture proportions. Then, bold Hardy-Weinberg equilibrium (HWE), the probability if observing the genotype G _i at site i is:

$$ p(G_{i} |\, f_{i}) = \left\{ \brainstorm{array}{lll} {(1-f_{i})}^{2} && \text{if}~~ G_{i} = 0 \\ 2 f_{i} (1-f_{i}) && \text{if}~~ G_{i} = 1 \\ {f_{i}}^{2} && \text{if}~~ G_{i} = 2 \end{array}\right. $$

((i))

For a given vector of admixture proportions, the log-likelihood of the observed genotypes thou for an private can exist defined as:

$$ Fifty(A) = \sum_{i=one}^{n} \text{ln} (Pr(G_{i} = g_{i} | \,f_{i})) $$

((2))

where chiliad _i is the observed genotype at site i. The above likelihood can be also exist written as a role of the genotype at each site every bit

$$L(A) = \left[ \sum_{i=1}^{n} g_{i} \text{ln}(f_{i}) + (2-g_{i})\text{ln}(i-f_{i}) \right] + C $$

where C is a constant.

The higher up formula assumes that all SNPs are contained or in linkage equilibrium with each other. In practice, SNPs can be pruned to reduce the linkage disequilibrium (LD) between the markers [9]. Given the matrix of allele frequencies q _ij (1≤i≤n and 1≤j≤one thousand) for k populations, our goal is to decide the vector A=[ a _ane,a ₂,…,a _k ] of admixture proportions that maximizes L(A) subject to the constraints a _j ≥0 and \(\sum _{j} a_{j} = ane\).

Maximizing the likelihood using the BFGS method

The likelihood function defined above is identical to the likelihood function used in previous methods [8,9] to update the admixture proportions given the allele frequencies. Our goal is to develop a computationally fast method for optimizing the likelihood function. The constraints on the admixture proportions (a _j ≥0 and \(\sum _{j} a_{j} = 1\)) make information technology hard to utilize standard optimization techniques. ADMIXTURE uses sequential quadratic programming combined with a quasi-Newton acceleration method to optimize the likelihood function. We utilize the Broyden-Fletcher-Goldfarb-Shanno (BFGS) method to optimize the likelihood function. The BFGS algorithm [23] is a popular quasi-Newton method for solving non-linear optimization issues that utilizes the first derivatives of the likelihood function and approximates the Hessian matrix of the second derivatives.

The constraint \(\sum _{j} a_{j} = 1\) can be addressed by replacing a _j with \(\frac {a_{j}}{S(a)}\) in the log-likelihood part where Due south(a) denotes the sum of the admixture coefficients. This corresponds to scaling the individual admixture coefficients by their sum. The showtime derivates of the likelihood function can be calculated as:

$$\frac{\partial L(A)} { \fractional a_{j}} = \sum_{i=i}^{n} \left[ \frac{g_{i} q_{ij}}{f_{i}} + \frac{(2-g_{i})(1-q_{ij})}{S(a) -f_{i}}\right] - \frac{2n}{S(a)} $$

To optimize the log-likelihood function, nosotros utilized the open up source implementation of the L-BFGS-B algorithm [24]. This method can handle simple box constraints required for our optimization problem (0≤a _j ≤1 for each admixture coefficient).

Genotype likelihoods for sequence data

In the previous section, we assumed that high quality genotypes determined via genotyping arrays are available. However, it may non be possible to decide an private's genotypes with high precision from sequence information, specially if the depth of coverage is low. For each SNP, the information almost the unobserved genotypes that is contained in the aligned reads covering the SNP tin can exist summarized using genotype likelihoods. These genotype likelihoods stand for to the probability of observing the sequence reads conditional on the genotype at the site. One time the sequence reads accept been aligned to the genome, we can determine the genotype likelihoods for each potential genotype at each site of interest using the base of operations quality values of the individual reads. Several methods for adding of genotype likelihoods have been proposed in the context of SNP calling from high-throughput sequence data [25-27]. We prefer an approach that is similar to these models. Let \(\mathcal {R} = \{ R_{1},R_{ii},\ldots R_{n}\}\) stand for the set of aligned reads roofing a SNP. Let a and b be the 2 alleles at this position.

Bold independence between sequencing errors from multiple reads, we can define the genotype likelihoods every bit:

$$ {\begin{aligned} Pr\left({\mathcal{R}}| G_{i} = one thousand\right) =&\; \prod_{j,R_{j} = a} \left\{ r(1-e_{j}) + (1-r)e_{j} \right\}\\ & \times \prod_{j,R_{j} = b} \left\{ (i-r)(ane-e_{j}) + {re}_{j}) \right\} \end{aligned}} $$

((3))

where yard=(0,ane,ii) is the number of a alleles and \(r = \frac {g}{two}\) is the probability of sampling the chromosome with the 'a' allele. This assumes equal probability of sampling the a and b for individuals who are heterozygous. For sequence data, the probability of sampling the reference allele can be slightly greater than 50% due to mapping bias. However, this should not significantly affect the interpretation of the admixture coefficients. The sequencing error probability, e _j , can be estimated using the respective base of operations quality value q _j as \(ten^{-0.one \times q_{j}}\phantom {\dot {i}\!}\). With these definitions, we can define the log-likelihood L(A), i.due east. the log of the probability of observing the sequence reads provisional on the admixture proportions A as:

$$ L(A) = \sum_{i=1}^{northward} \text{ln} \left[ \sum_{k=0}^{2} Pr({\mathcal{R}}_{i} | G_{i} = g) Pr(G_{i} = g | A) \correct] $$

((4))

where \({\mathcal {R}}_{i}\) is the set of aligned reads covering the site i.

Parsimonious estimation of admixture coefficients

Given multiple reference populations, the maximum likelihood approach finds the admixture coefficients for each population that maximize the given likelihood role. Populations with a non-cipher admixture coefficient are likely to contribute to the individual'due south genotypes. However, in the presence of a large number of reference populations, some of which are closely related, it tin can be difficult to reliably guess which populations contribute significantly to an private'due south ancestry. Imprecise allele frequency estimates due to incomplete sampling or the absence of correct parental populations tin can as well result in non-zero admixture coefficients associated with populations that do not actually contribute to the individual's genetic ancestry. One arroyo to identifying the populations that contribute significantly to the individual's genetic ancestry is to judge standard errors for each estimated admixture coefficient using a bootstrap approach. The ADMIXTURE method [nine] uses a block bootstrap to estimate standard errors. However, this is computationally enervating since the likelihood maximization needs to be performed for several hundred resamples. We implemented a simple merely rigorous approach to make up one's mind a parsimonious set of admixture coefficients for an individual by iteratively removing population(s) for which a non-zip admixture coefficient does not improve the model fit significantly. This method is analogous to the backward elimination method for variable selection. Nosotros detect the population for which setting the admixture coefficient to nothing does not reduce the best-fit likelihood significantly using the likelihood ratio statistic. The admixture coeffcient for this population is fixed to exist 0 and this procedure is repeated iteratively. A description of the method is equally follows:

1. 1.

   Calculate the maximum likelihood guess for the admixture coefficients A

2. two.

   For each population j with a non-zero admixture coefficient, summate δ _j =L _max −L _−j obtained by calculating the maximum likelihood fit with the j-th admixture coefficient constrained to be 0

3. 3.

   determine the population p with the smallest value of δ _j

4. 4.

   Set for admixture coefficient p to exist 0 if δ _p <T where T is a threshold based on the likelihood ratio test

5. 5.

   Echo Steps (2)-(four) until possible

The threshold T can be chosen according to the desired level of parsimony in the admixture coefficients. We use a threshold value of T=5.414 which corresponds to a p-value threshold of 0.001 using the chi-square distribution with ane caste of liberty.

Estimating ancestry from pooled sequence data

High-throughput sequencing of targeted genomic loci in large numbers of cases and controls is an effective approach for identifying rare genetic variants that affect risk for illness. Although next-generation sequencing technologies have the throughput to generate enough reads for thousands of individuals, the toll of preparing individual DNA sequencing libraries prior to sequencing limits the number of individuals that can be sequenced. A toll-effective approach for sequencing thousands of individuals is to pool Dna, in equi-molar proportions, from multiple individuals together to form pools and sequence the pools, instead of individuals [28]. This pooled sequencing arroyo has been used successfully to identify disease associated rare variants for a number of complex diseases: type i diabetes [29], inflammatory bowel disease [thirty], rheumatoid arthritis [31] and anorexia nervosa [32].

Dna pooling based association studies, similar to standard clan studies, also require some way of correcting for population stratification. If genotype information from whole-genome arrays or at beginnings informative markers is available for each individual, this tin exist used to identify outlier individuals and exclude them from the pooled sequencing. However, generating individual level genotype data is plush and reduces the cost effectiveness of pooling based association studies. Therefore, a method that can judge the average ancestry of each puddle directly from the sequence reads would be valuable. The pooled admixture coefficients tin can be used to remove pools with very different ancestry compared to other pools from the association analysis. In add-on, the admixture coefficients can be used as covariates in association analysis thereby bookkeeping for population stratification. With this motivation, we extended our method to work with pooled sequence data derived from loftier-throughput sequencing of 'bogus' Deoxyribonucleic acid pools derived by pooling Deoxyribonucleic acid in equal proportions from multiple individuals.

Like to diploid individuals, we represent the genotype Chiliad _i of a puddle as the number of 'a' alleles or chromosomes at this site. Thus, if the pool has p diploid individuals, the number of potential pooled genotypes at a bi-allelic site is 2p+i. Due to errors in Dna quantification, there is likely to be some variance in the proportion of each private's DNA in a puddle. Kim et al. [33] used a gamma distribution to model the variance in the DNA proportions from each individual in a pool. All the same, it is difficult to estimate the proportions without individual genotype data [34]. For ancestry cess, it is a reasonable approximation to assume that each individual contributes equal corporeality of Dna to a pool.

Given the aligned sequence reads for each pool, nosotros can calculate the genotype likelihoods \(Pr({\mathcal {R}} | G_{i} = g)\) (0≤g≤iip) every bit follows:

$$Pr({\mathcal{R}}| G_{i} = g) = \prod_{j,R_{j} = a} f_{j} \prod_{j,R_{j} = b} (1-f_{j}) $$

where

$$ f_{j} = \frac{1000}{2p}(1-e_{j}) + \left(1-\frac{thou}{2p} \right)e_{j} $$

These pooled genotype likelihoods can then exist used to summate the log likelihood L(A) as defined in equation 4.

Results and discussion

Reference populations and allele frequencies

The HapMap 3 information ready [12] includes ane,397 individuals from eleven different populations that take been genotyped using the Illumina 1M and the Affymetrix 6.0 arrays. We downloaded genotypes for all the individuals in this dataset from the HapMap project website (http://hapmap.ncbi.nlm.nih.gov/) Nosotros removed related individuals and pruned a subset of SNPs based on Linkage Disequilibrium (LD) (r ² threshold of 0.3) using the Plink software tool [35] to generate a reduced prepare of 249,075 SNPs with genotypes for 1198 unrelated individuals. For each population, allele counts were calculated for each SNP using plink (–freq control) and allele frequencies were estimated from the allele counts.

Simulations

To assess how accurately our method can recover the truthful admixture coefficients, we simulated admixed individuals using allele frequencies from the HapMap 3 dataset. We faux an inter continental admixture scenario with admixture between the CEU, CHB and YRI populations. For each private, the admixture coefficients for the three populations were sampled uniformly at random from a 2-dimensional unit simplex (x _ane+x _ii+x ₃=1) and the genotypes were simulated using the genotype likelihoods defined in Equation ane. Nosotros faux genotypes for 100 individuals and estimated admixture coefficients using our method. For each simulated individual, nosotros used the root mean foursquare error (RMSE) to assess the accuracy of the admixture coefficients estimated by our method. The RMSE was calculated using the post-obit formula:

$$ RMSE (\chapeau{a},a) = \sqrt { \frac{1}{k} \sum\limits_{i=1}^{k} { (\hat{a_{i}} -a_{i})}^{2}} $$

where k is the number of reference populations and a _i is the admixture coefficient associated with population i. Results from the simulations showed that iAdmix was able to estimate the admixture coefficients quite accurately with a mean RMSE of 0.0028 (range from 0.0004-0.015).

The simulations utilized the same set of allele frequencies to estimate the admixture coefficients using iAdmix that were used to simulate the individuals. This does not capture the variance in the allele frequencies due to finite sample size of the reference populations. To mimic a realistic setting with noisy population allele frequencies, nosotros sampled genotypes for a finite number of individuals (n = 100) for each population and used the allele frequencies estimated from this sample for admixture analysis using iAdmix. The genotypes were sampled using the true allele frequencies. Results using the noisy allele frequencies indicated that admixture proportions associated with different continents (Europe, Eastern asia and Africa) can be estimated with high accuracy (hateful RMSE = 0.0037) but information technology is difficult to estimate the admixture coefficients associated with populations inside each continental group. For example, we observed that the European admixture component estimated past our method is split betwixt the CEU and TSI populations. This is likely due to the low differentiation between some populations from the same continent (east.chiliad. Fst betwixt the CHB and CHD populations from East Asia is 0.001 while the Fst between the CEU and TSI populations is 0.004 [12]). Nosotros besides estimated admixture coefficients using the ADMIXTURE program run in supervised mode using the false genotypes for 100 individuals per population as the reference clusters. The hateful RMSE averaged over 100 simulations was 0.0031, marginally lower than the mean RMSE for our method. Overall, the simulations indicated that our method can estimated admixture coefficients associated with different continental populations with high accurateness.

Analysis for Mozabite individuals in the HGDP

To evaluate the ability of our method to approximate admixture coefficients from existent data, we analyzed genotype information from 25 individuals from the Mozabite population in the Homo Genome Variety Panel (HGDP) [xi]. We downloaded Illumina genotypes at ∼ 650,000 markers for these individuals from the HGDP website and 114,056 of these markers were in mutual with the reduced set of 249,075 SNPs from the HapMap dataset. We ran our method, iAdmix, on each individual separately using allele frequencies from 8 HapMap populations (the iii admixed populations GIH, MXL and ASW were excluded). The admixture estimates (run across Figure 1(a)) show that all the individuals are admixed with both European and African components of ancestry. Cost et al. [36] analyzed the aforementioned set of individuals using their local beginnings inference method, HAPMIX, and estimated that the Mozabite individuals have approximately 78% beginnings from a European-related population and 22% from a population related to sub-Saharan Africa. Our estimates of admixture coefficients are consequent with the local ancestry based estimates.

Figure 1

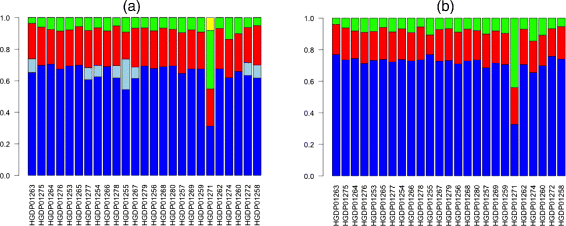
Admixture proportions for 25 Mozabite individuals. The coefficients were estimated using allele frequencies from the HapMap reference populations and using two methods: iAdmix (a) and ADMIXTURE (b). The population labels are as follows: TSI (bluish), CEU (light blueish), MKK (red), YRI (greenish) and LWK (yellow).

Total size image

For comparison, nosotros likewise ran ADMIXTURE (in supervised mode using the HapMap reference panel of individuals) on the same dataset (encounter Figure 1(b)). The European and African admixture estimates for each individual were highly consequent betwixt the two methods. For some individuals, the European component of ancestry using our method was split betwixt the TSI and CEU populations. This could reflect one important deviation between the two methods in how they utilize data from reference individuals. Our method finds a maximum likelihood estimate of the admixture coefficients for each individual using the fixed ready of allele frequencies. In contrast, ADMIXTURE, in the supervised mode, utilizes data for all individuals (both the reference populations and the individual(s) being analyzed) to gauge the allele frequencies for each cluster or population and maximize the likelihood function summed across all individuals. Therefore, the allele frequencies are determined not only by the genotypes of the reference individuals only as well by the private(southward) that are analyzed for admixture. To confirm this, nosotros estimated allele frequencies by running ADMIXTURE twice: (ane) using 800 reference individuals fake using allele frequencies for 8 HapMap populations (100 individuals per population, run across previous section) and (ii) 800 reference individuals and 1 additional private with 100% CEU ancestry imitation using the HapMap allele frequencies. Subsequently, nosotros used our method to estimate admixture coefficients for the simulated CEU individual using the two sets of allele frequencies separately. We found that using the outset set of allele frequencies, the admixture coefficients for both CEU and TSI were non-cypher. In contrast, using the second set of allele frequencies, but the CEU admixture coefficient was non-cypher. This was similar to the results observed in the assay of the Mozabite data and provided an empirical validation of our hypothesis regarding the deviation in the admixture coefficients estimated by the ii methods.

Estimating ancestry from Dna sequence reads

Next, nosotros assessed the performance of our method on sequence data from the g Genomes Project [18]. For this, we utilized 6 individuals from the ASW population (individuals with African beginnings in SouthWest Usa) whose genomes have been subjected to both low coverage whole-genome sequencing and exome sequencing on the Illumina sequencing platform. We downloaded bam files with the aligned sequence reads for the 6 individuals from the 1000 Genomes Projection website (ftp://ftp-trace.ncbi.nih.gov/1000genomes/ftp/data/). For each bam file, genotype likelihoods (defined in equation (3)) were calculated at each site in the HapMap3 allele frequency data that had one or more reads covering it. We analyzed the distribution of the depth of coverage across the sites using the reads for ane individual (come across Effigy 2). Interestingly, the exome data had at least one read covering 78.2% of the 249,075 sites. In comparing, 95.8% of the sites had not-nada read depth using the low-coverage data. We calculated admixture proportions using iAdmix for each of the 6 individuals (see Table i) and summed the admixture proportions associated with population within 3 continental groups (African, European and East Asian). We observed very high cyclopedia betwixt the admixture proportions estimated using the low-coverage and the exome sequence data (root mean foursquare difference between the 2 admixture vectors for each individual ranged from 0.003-0.0064). Unexpectedly, 1 individual (NA19625) was estimated to accept significant Due east Asian related ancestry (16.5%). Analysis of genotype data from this private carried out in the HapMap project also indicated the presence of East Asian ancestry [12], confirming our results. Overall, these results demonstrate the feasibility of straight estimating beginnings from both whole-genome and targeted sequencing experiments.

Figure 2

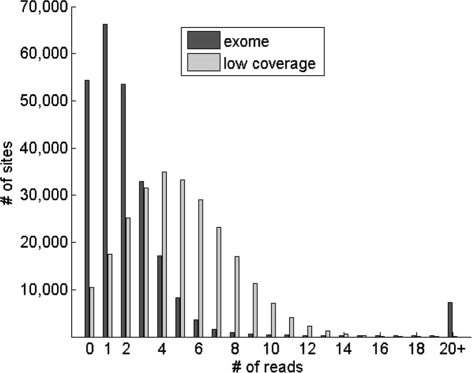
Distribution of the number of reads covering the 249,075 polymorphic sites in the HapMap3 allele frequency panel using low-coverage whole-genome and exome sequence data from one private (NA19704) sequenced in the thou Genomes Project.

Total size image

Table ane Comparison of admixture estimates for individuals from ASW population

Total size tabular array

Analysis of pooled sequence information

To assess the power of our method to estimate admixture coefficients from pooled sequence information, nosotros utilized exome sequence data from the k Genomes Project [eighteen] to simulate pools. We downloaded bam files containing exome sequence data for individuals from a European population (Great britain, GBR), an E Asian population (Southern Han Chinese, CHS) and an African population (Luhya, LWK). We created four pools by merging the reads from the individual bam files. The starting time pool contained reads from 20 GBR individuals, the second puddle was composed of reads from xix GBR individuals and 1 CHS private, a third pool independent reads from nineteen GBR individuals and 1 LWK individual, and the quaternary pool was comprised of reads from 18 GBR individuals, i CHS individual and i LWK individual. The rationale for creating these false pools was to assess the ability of our method to determine if the ancestry of the individuals in a pool was homogeneous or if 1 or more individuals in a pool had ancestry from other populations. This would be useful in a case-control clan study to identify pools with non-homogeneous ancestry. To mimic the calibration of a targeted sequencing experiment, nosotros utilized reads that mapped to chromosome eleven only.

For each pool, nosotros calculated the admixture coefficients using our method and the allele frequencies from the HapMap dataset. To maximize overlap between the sequence reads and the variants in the HapMap dataset, we utilized all genotyped SNPs instead of the LD pruned subset of SNPs.

For the pool with the xx GBR individuals, but the European populations (CEU and TSI) had non-goose egg admixture coefficients. For the pool that included reads from a single CHS individual, an E Asian population (CHD) had a non-zero admixture coefficient that was statistically significant (see Table 2). Similarly, we observed a non-zero African admixture coefficient for the pool with one LWK private and two non-nil admixture coefficients (respective to East Asian and African populations) in the pool with ii non-European ancestry individuals (Table 2). To appraise the ability to detect admixture in larger sized pools, we simulated pools with 40 individuals (39 GBR and one CHS) and 60 individuals (59 GBR and 1 CHS). Our method was able to detect the presence of E Asian beginnings in the pool with xl individuals (expected = 0.0257, observed = 0.0295) as well as the pool with 60 individuals (expected = 0.0164, observed = 0.0207). These results demonstrated that our method can reliably detect the presence of individuals with not-European ancestry in a pool of European ancestry individuals using sequence reads from the pool.

Table 2 Admixture coefficients for simulated pools

Full size table

The ability to estimate admixture coefficients is dependent on the number of variants with genotype information from the sequence reads. For each pool, the number of SNPs that had non-zilch coverage was ∼ 72,000 and of these, ∼ 3,300 SNPs had an average coverage of xx × or greater per individual. To assess the accuracy of estimating admixture coefficients every bit a function of the number of SNPs, we analyzed the puddle with 19 GBR individuals and ane CHS private (East Asian admixture coefficient = 0.05) with random subsets of SNPs with varying percentage (v-40%) of the total numbers of SNPs. Not surprisingly, the standard difference of the admixture coefficient for the E Asian ancestry was high (0.0096 for fifty samples) at 5% and decreased to 0.0032 as the pct of SNPs used increased to xl% (see Additional file one: Figure S1).

Implementation and running fourth dimension

To optimize the likelihood office, nosotros utilized the open source implementation of the 50-BFGS-B algorithm past Zhu and colleagues [37]. The computational complexity for each iteration of the BFGS algorithm is O(north k p) where n is the number of SNPs, thou is the number of reference populations and p is the pool size. However, the total run time depends on the number of iterations required for the convergence of the BFGS optimization. The BFGS method was run until the departure between successive log-likelihoods was less than 0.00001. The same convergence benchmark has been used by previous methods [9]. In all the evaluations using both real and simulated data, the number of iterations for convergence was typically xx-30 and did not exceed 50. We initialized the admixture coefficients with random values between 0 and i. Empirical evaluation showed that the optimization converged to the same final solution regardless of the initial admixture coefficients.

The main method was implemented in C and the input and output files were processed using Python. To summate genotype likelihoods for variant sites from BAM files, we implemented a custom plan using the Samtools library [38].

Our method analyzes one sample at a time and the average run time per sample for our method (averaged beyond 100 simulations) was 5.ii seconds for the initial BFGS optimization and 14.eight seconds for the full method including the parsimonious interpretation of admixture coefficients. In comparing, the average run time for ADMIXTURE in supervised mode was 87.6 seconds per sample. To assess the ability of our method to approximate admixture proportions associated with a big number of reference populations, we estimated admixture proportions for the Mozabite individuals using allele frequencies at xvi,433 SNPs derived from a reference console of 26 global populations [39]. Our method was able to estimate admixture coefficients with an average run fourth dimension of vi.4 seconds per individual compared to 57 seconds for a supervised ADMIXTURE run (results not shown). All evaluations were washed on a single core of an Intel Xeon processor (ii.6 GHz) with 64-bit Linux organisation.

Conclusions

In this paper, we have described a computationally fast and efficient method, iAdmix, which tin can be used to infer global andmixture proportions from genotype or sequence data using a reference prepare of population allele frequencies. This method employs the BFGS optimization algorithm, which makes it possible to estimate an individual'south admixture proportions from whole-genome genotype data in seconds even in the presence of multi-way admixture. Using simulations, nosotros accept demonstrated that our method is able to deconvolute admixture associated with multiple continental populations with comparable accuracy and significantly better speed then existing methods. The increased computational efficiency is the primary accelerate of our method as it allows united states to estimate admixture proportions associated with a large number of bequeathed populations and too to run iAdmix iteratively in order to obtain parsimonious admixture estimates.

The likelihood model for estimating the admixture proportions assumes Hardy-Weinberg equilibrium (HWE) to calculate the genotype likelihoods. This model tin be extended to capture deviations from HWE due to inbreeding [40] and simultaneously judge the admixture coefficients and the inbreeding coefficient. This may be useful for analysis of individual genomes from populations with some level of inbreeding in order to place illness causing mutations. Preliminary results indicate that the admixture coefficients are robust to deviations from HWE (results not shown) and we plan to investigate this further in the future.

Another fundamental advantage of our method is that it uses allele frequencies rather than private genotypes. Therefore it tin can leverage allele frequencies for populations for which no 'pure' or non-admixed exist or are difficult to obtain. For example, Bustamante and colleagues [41] have estimated allele frequencies for Native American populations using local beginnings analysis of populations sequenced in the 1000 Genomes Project that tin be used for admixture analysis of Hispanic individuals. The accurateness of ancestry inference by our method relies on the availability of accurate allele frequencies for a large number of reference populations. In this paper, we used allele frequencies calculated from samples collected every bit part of the HapMap3 projection. While an impressive undertaking, the populations contained in this resource are a limited sampling of the global population diversity. A more comprehensive panel would exist extremely useful as information technology would let for a more meaningful and accurate inference. The 1000 Genomes project is generating sequence and genotype information on more than 25 dissimilar populations and once completed, it would be a valuable resources for reference human populations. Many populations have already been sampled by diverse research groups, and a large number of publicly available genotype datasets exist. The collation of these disparate resource is an important topic for future piece of work.

The described method addresses the trouble of estimating the genome-wide average or global ancestry of an individual. In many applications, local ancestry, i.e., the ancestry of a chromosomal segment that has been inherited from an antecedent associated with a unmarried parental population, is of interest. Notwithstanding, this is a difficult problem and existing methods for inference of local ancestry typically consider but two or three ancestral populations [36,42-44]. Our method was motivated by the need for estimating beginnings in sequencing based clan studies where global admixture estimates can be used as covariates in association analysis or to exclude outlier individuals. Sequencing data poses new challenges for admixture estimation just also presents opportunities for the development of methods that can exploit data present in sequence data that may be missing in genotype information, e.g. relating to rare or population-specific variants [45]. With the increasing use of high-throughput sequencing technologies, methods such as iAdmix and other recently adult methods [20-22,45] should prove useful for the assessment of ancestry in studies of human genetic variation and illness.

References

1. Luca, Menozzi P, Piazza A. The History and Geography of Human Genes. Princeton, NJ: Princeton Academy Press; 1994.

   Google Scholar

2. Rosenberg NA, Pritchard JK, Weber JL, Cann HM, Kidd KK, Zhivotovsky LA, et al. Genetic structure of homo populations. Science. 2002; 298(5602):2381–five.

   CAS  Commodity  PubMed  Google Scholar

3. Tang H, Jorgenson E, Gadde 1000, Kardia SL, Rao DC, et al. Racial admixture and its bear on on BMI and blood pressure level in African and Mexican Americans. Hum Genet. 2006; 119(vi):624–33.

   Article  PubMed  Google Scholar

4. Cardon LR, Palmer LJ. Population stratification and spurious allelic association. Lancet. 2003; 361(9357):598–604.

   Article  PubMed  Google Scholar

5. Marchini J, Cardon LR, Phillips MS, Donnelly P. The furnishings of homo population structure on large genetic association studies. Nat Genet. 2004; 36(5):512–7.

   CAS  Commodity  PubMed  Google Scholar

6. Price AL, Zaitlen NA, Reich D, Patterson N. New approaches to population stratification in genome-wide association studies. Nat Rev Genet. 2010; eleven(7):459–63.

   CAS  Commodity  PubMed  PubMed Central  Google Scholar

7. Pritchard JK, Stephens M, Donnelly P.Inference of population structure using multilocus genotype data. Genetics. 2000; 155(2):945–59.

   CAS  PubMed  PubMed Central  Google Scholar

8. Tang H, Peng J, Wang P, Risch NJ. Estimation of individual admixture: belittling and study design considerations. Genet Epidemiol. 2005; 28(4):289–301.

   Article  PubMed  Google Scholar

9. Alexander DH, Novembre J, Lange Yard.Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 2009; xix(nine):1655–64.

   CAS  Commodity  PubMed  PubMed Key  Google Scholar

10. Patterson N, Price AL, Reich D. Population construction and eigenanalysis. PLoS Genet. 2006; two(12):e190.

11. Li JZ, Absher DM, Tang H, Southwick AM, Casto AM, Ramachandran S, et al. Worldwide human relationships inferred from genome-broad patterns of variation. Science. 2008; 319(5866):1100–four.

    CAS  Article  PubMed  Google Scholar

12. Altshuler DM, Gibbs RA, Peltonen Fifty, Altshuler DM, Gibbs RA, Peltonen L, et al. Integrating common and rare genetic variation in diverse human populations. Nature. 2010; 467(7311):52–8.

    CAS  Article  PubMed  Google Scholar

13. Nelson MR, Bryc Chiliad, King KS, Indap A, Boyko AR, Novembre J, et al. The Population Reference Sample, POPRES: a resources for population, disease, and pharmacological genetics research. Am J Hum Genet. 2008; 83(3):347–58.

    CAS  Article  PubMed  PubMed Central  Google Scholar

14. Xing J, Watkins WS, Witherspoon DJ, Zhang Y, Guthery SL, Thara R, et al. Fine-scaled man genetic structure revealed by SNP microarrays. Genome Res. 2009; 19(5):815–25.

    CAS  Article  PubMed  PubMed Central  Google Scholar

15. Xing J, Watkins WS, Shlien A, Walker Eastward, Huff CD, Witherspoon DJ, et al. Toward a more uniform sampling of human genetic diversity: a survey of worldwide populations by high-density genotyping. Genomics. 2010; 96(iv):199–210.

    CAS  Commodity  PubMed  PubMed Central  Google Scholar

16. Alexander DH, Lange G. Enhancements to the ADMIXTURE algorithm for individual beginnings estimation. BMC Bioinformatics. 2011; 12:246.

17. Kiezun A, Garimella K, Exercise R, Stitziel NO, Neale BM, McLaren PJ, et al. Exome sequencing and the genetic basis of circuitous traits. Nat Genet. 2012; 44(half dozen):623–30.

    CAS  Commodity  PubMed  PubMed Fundamental  Google Scholar

18. Abecasis GR, Auton A, Brooks LD, DePristo MA, Durbin RM, Handsaker RE, et al. An integrated map of genetic variation from 1,092 human being genomes. Nature. 2012; 491(7422):56–65.

    Commodity  CAS  PubMed  Google Scholar

19. Guo Y, Long J, He J, Li CI, Cai Q, Shu XO, et al. Exome sequencing generates loftier quality data in non-target regions. BMC Genomics. 2012; 13:194.

20. Skotte L, Korneliussen TS, Albrechtsen A. Estimating individual admixture proportions from next generation sequencing data. Genetics. 2013; 195(3):693–702.

    CAS  Article  PubMed  PubMed Central  Google Scholar

21. Hu Y, Willer C, Zhan X, Kang HM, Abecasis GR. Accurate local-ancestry inference in exome-sequenced admixed individuals via off-target sequence reads. Am J Hum Genet. 2013; 93(5):891–ix.

    CAS  Commodity  PubMed  PubMed Fundamental  Google Scholar

22. Wang C, Zhan X, Bragg-Gresham J, Kang HM, Stambolian D, Chew EY, et al. Beginnings estimation and control of population stratification for sequence-based clan studies. Nat Genet. 2014; 46(4):409–15.

    CAS  Article  PubMed  PubMed Central  Google Scholar

23. Nocedal J, Wright SJ. Numerical optimization: Springer; 2000. [http://www.amazon.com/exec/obidos/redirect?tag=citeulike07-20&path=ASIN/0387987932]

24. Byrd R, Lu P, Nocedal J, Zhu C. A Express Memory Algorithm for Bound Constrained Optimization. SIAM J Sci Comput. 1995; xvi(5):1190–208. [http://epubs.siam.org/doi/abs/10.1137/0916069]

    Article  Google Scholar

25. Li H, Ruan J, Durbin R. Mapping short Dna sequencing reads and calling variants using mapping quality scores. Genome Res. 2008; 18(11):1851–8.

    CAS  Article  PubMed  PubMed Central  Google Scholar

26. Li R, Li Y, Fang 10, Yang H, Wang J, Kristiansen K, et al. SNP detection for massively parallel whole-genome resequencing. Genome Res. 2009; 19(vi):1124–32.

    CAS  Article  PubMed  PubMed Central  Google Scholar

27. Bansal V, Harismendy O, Tewhey R, Murray SS, Schork NJ, Topol EJ, et al. Authentic detection and genotyping of SNPs utilizing population sequencing data. Genome Res. 2010; 20(4):537–45.

    CAS  Article  PubMed  PubMed Central  Google Scholar

28. Bansal V, Tewhey R, Leproust EM, Schork NJ. Efficient and toll constructive population resequencing past pooling and in-solution hybridization. PLoS I. 2011; 6(3):e18353.

29. Nejentsev S, Walker N, Riches D, Egholm 1000, Todd JA. Rare variants of IFIH1, a gene implicated in antiviral responses, protect against type 1 diabetes. Science. 2009; 324(5925):387–9.

    CAS  Commodity  PubMed  PubMed Central  Google Scholar

30. Rivas MA, Beaudoin Grand, Gardet A, Stevens C, Sharma Y, Zhang CK, et al. Deep resequencing of GWAS loci identifies independent rare variants associated with inflammatory bowel affliction. Nat Genet. 2011; 43(11):1066–73.

    CAS  Article  PubMed  PubMed Central  Google Scholar

31. Diogo D, Kurreeman F, Stahl EA, Liao KP, Gupta N, Greenberg JD, et al. Rare, low-frequency, and common variants in the protein-coding sequence of biological candiyear genes from GWASs contribute to take a chance of rheumatoid arthritis. Am J Hum Genet. 2013; 92:xv–27.

    CAS  Article  PubMed  PubMed Central  Google Scholar

32. Scott-Van Zeeland AA, Bloss CS, Tewhey R, Bansal V, Torkamani A, Libiger O, et al. Evidence for the role of EPHX2 gene variants in anorexia nervosa. Mol Psychiatry. 2014; nineteen(half dozen):724–32.

    CAS  Article  PubMed  Google Scholar

33. Kim SY, Li Y, Guo Y, Li R, Holmkvist J, Hansen T, et al. Blueprint of association studies with pooled or un-pooled next-generation sequencing data. Genet Epidemiol. 2010; 34(5):479–91.

    Commodity  PubMed  PubMed Central  Google Scholar

34. Eskin I, Hormozdiari F, Conde L, Riby J, Skibola CF, Eskin E, et al. eALPS: estimating abundance levels in pooled sequencing using bachelor genotyping data. J Comput Biol. 2013; xx(11):861–77.

    CAS  Article  PubMed  PubMed Central  Google Scholar

35. Purcell South, Neale B, Todd-Brown Thousand, Thomas 50, Ferreira MA, Bender D, et al. PLINK: a tool set up for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007; 81(3):559–75.

    CAS  Commodity  PubMed  PubMed Central  Google Scholar

36. Price AL, Tandon A, Patterson N, Barnes KC, Rafaels N, Ruczinski I, et al. Sensitive detection of chromosomal segments of singled-out ancestry in admixed populations. PLoS Genet. 2009; 5(half dozen):e1000519.

37. Zhu C, Byrd RH, Lu P, Nocedal J. Algorithm 778: L-BFGS-B: fortran subroutines for big-calibration bound-constrained optimization. ACM Trans Math Softw. 1997; 23(4):550–60.

    Article  Google Scholar

38. Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N, et al. The sequence alignment/map format and SAMtools. Bioinformatics. 2009; 25(xvi):2078–ix.

    Commodity  CAS  PubMed  PubMed Cardinal  Google Scholar

39. Libiger O, Schork NJ. A method for inferring an individual'southward genetic ancestry and degree of admixture associated with six major continental populations. Front Genet. 2012; three:322.

40. Vieira FG, Fumagalli Chiliad, Albrechtsen A, Nielsen R. Estimating inbreeding coefficients from NGS data: Touch on on genotype calling and allele frequency interpretation. Genome Res. 2013; 23(eleven):1852–61.

    CAS  Article  PubMed  PubMed Fundamental  Google Scholar

41. Gravel Southward, Zakharia F, Moreno-Estrada A, Byrnes JK, Muzzio M, Rodriguez-Flores JL, et al. Reconstructing Native American migrations from whole-genome and whole-exome data. PLoS Genet. 2013; ix(12):e1004023.

42. Sankararaman S, Sridhar Southward, Kimmel K, Halperin E.Estimating local ancestry in admixed populations. Am J Hum Genet. 2008; 82(2):290–303.

    CAS  Article  PubMed  PubMed Key  Google Scholar

43. Tang H, Coram G, Wang P, Zhu X, Risch N.Reconstructing genetic ancestry blocks in admixed individuals. Am J Hum Genet. 2006; 79:1–12.

    CAS  Article  PubMed  PubMed Fundamental  Google Scholar

44. Maples BK, Gravel S, Kenny EE, Bustamante CD. RFMix: a discriminative modeling approach for rapid and robust local-ancestry inference. Am J Hum Genet. 2013; 93(ii):278–88.

    CAS  Commodity  PubMed  PubMed Key  Google Scholar

45. Dark-brown R, Pasaniuc B. Enhanced methods for local ancestry assignment in sequenced admixed individuals. PLoS Comput Biol. 2014; 10(iv):e1.003555.

Download references

Acknowledgements

Dr Bansal is supported by a grant 1R21HG007430 from NIH.

Author information

Affiliations

1. Department of Pediatrics, University of California San Diego, 9500 Gilman Drive, La Jolla, 92093, CA, USA

   Vikas Bansal

2. Scripps Translational Science Plant, 3344 North Torrey Pines Courtroom, La Jolla, 92037, CA, USA

   Vikas Bansal & Ondrej Libiger

3. Current address: MD Revolution, San Diego, CA, U.s.

   Ondrej Libiger

Corresponding author

Correspondence to Vikas Bansal.

Boosted information

Competing interests

The authors declare that they have no competing interests.

Authors' contributions

VB designed the method, implemented the software, analyzed information and wrote the paper. OL analyzed data and wrote the paper. Both authors read and approved the final manuscript.

Additional file

Rights and permissions

This is an Open Admission article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/iv.0), which permits unrestricted use, distribution, and reproduction in whatsoever medium, provided the original work is properly credited. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the information fabricated bachelor in this article, unless otherwise stated.

Reprints and Permissions

About this article

Cite this article

Bansal, V., Libiger, O. Fast individual ancestry inference from DNA sequence data leveraging allele frequencies for multiple populations. BMC Bioinformatics xvi, 4 (2015). https://doi.org/ten.1186/s12859-014-0418-7

Download citation

• Received: 08 October 2014

• Accepted: 10 December 2014

• Published: 16 Jan 2015

• DOI : https://doi.org/ten.1186/s12859-014-0418-7

Keywords

• Admixture estimation
• Loftier-throughput sequencing
• Allele frequencies
• Maximum likelihood
• Beginnings
• BFGS algorithm

Source: https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-014-0418-7

Posted by: mcgrathextured.blogspot.com

Share this post